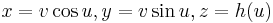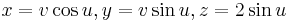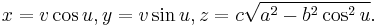Right conoid

In geometry, a right conoid is a ruled surface generated by a family of straight lines that all intersect perpendicularly a fixed straight line, called the axis of the right conoid.

In the space Cartesian coordinate system, if we take the z-axis as the axis of a right conoid, then the right conoid can be represented by the following parametric equations

x=v\cos u, y=v\sin u, z=h(u) \,

where h(u) is some function for representing the height of the moving line.

Examples

A typical example of right conoids is given by the parametric equations:

x=v\cos u, y=v\sin u, z=2\sin u\,

Figure 2 shows how the coplanar lines generate the right conoid.

Other right conoids include:

1. Helicoid: 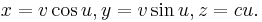x=v\cos u, y=v\sin u, z=cu.\,

2. Whitney umbrella: 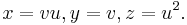x=vu, y=v, z=u^2.\,

3. Wallis’s conical edge: x=v\cos u, y=v \sin u, z=c\sqrt{a^2-b^2\cos^2u}.\,

4. Plücker’s conoid: 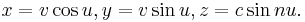x=v\cos u, y=v\sin u, z=c\sin nu.\,

5. hyperbolic paraboloid: 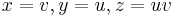x=v, y=u, z=uv\, (with x-axis and y-axis as its axes).

See also

External links